2.2.5    ネットワークを捉える

2.2.5.1  層をまたぐスケッチ：複雑性の観察の差を捉えるクロス表

　ゲームの概念には多層性がある。そうであるとして、では、その層をどう切り分け、どう接続して考えることができるのだろうか。 

　たとえば、「ルール」や「目標」といった要素をゲームの概念の重要な側面として語る議論と、「積極的学習行為」のような高次の複雑性をもった議論とはそのままでは、接続して考えることが難しい。

　この接続の難しさには、研究の作法の違いが関係している。ひとつは、分析哲学に代表されるように、論理的に扱いやすい水準の概念から議論を組み立てる態度である。もうひとつは、学際的に高い複雑性を引き受けながら、現象全体を描こうとする態度である。

　ただし、この問題は「学問分野間の翻訳不可能性」だけでは説明しきれない。繰り返し述べてきたように、むしろ複雑性の水準の差として捉え直すこともできる。

　たとえば、「ゲームにおける学習プロセス」を、目的・ルール・フィードバック・自発的参加といった要素の総合として記述するとしよう。このとき、目的やルールは基礎的（低次）な要素であり、学習プロセスはそれらの組み合わせとして現れる合成的（高次）な要素だ[1]。

　 その視点にたったうえで、多様な定義論を総合するような形で、試しにそれぞれの議論のレイヤーの差異をまとめたようなクロス表を作成してみれば下記のような表を例示することができるだろう。

表１：ゲームの概念の多層性

　この表では、縦軸に分析の複雑性の水準の違いをとり、横軸にユール(2005)が措定したような主体の水準を問題とする層構造[2]をとっている。B.合成的な分析概念は、概ねサットン＝スミス(1997)の「７つのレトリック」に対応しており、C.基礎的な分析概念は、概ねステンロス(2015)の挙げる論点に対応している。ユールの挙げる論点は、B 合成的な分析概念とC 基礎的な分析概念の水準にまたがっている。Bの合成的な分析概念は、Cの基礎的な分析概念のいくつかが合わさる形でできるようなものだ。この表は、多様な定義論の視点の違いと、分析の水準について説明しうるものにはなりうるだろう。

2.2.5.2  「階層」は自明か？

　ただし、この表のような縦軸の多層性の表現は、層の構造自体が、分析者の視点によって任意に変わりやすいものでもある。たとえば、MDAモデルに対応させて言うのならば、M（メカニクス）は環境／形式にあたり、A（エステティクス）はプレイヤーの認知的側面にあたるが、D（ダイナミクス）に該当する層がない[3]。

　さて、では階層性を仮定するとき、それはどのように捉えればよいのだろうか。

　創発の話をするにしても、モデル間の階層性のイメージは一致している、とは言いづらい。ある程度までシンプルな多層モデルを考えるとしても、どのような多層性を考えるかにも見解が分かれている。ゲームに関わる現象を多層化するモデルは様々なものが存在している。

　全てを詳細に紹介するには多すぎるが、すでに述べてきたいくつかの整理も含めて、表にして示しておこう[4]。

表２：ゲームに関する様々な多層モデル

　こうした階層のモデリングは区別を付けることによって何を強調したいのかが異なっている。ゲームデザインにおける重要な区別を導入したいのか、ゲームの表現内容の解釈を問題としたいのか、行為全体の基礎的なモデル化をしたいのか、ゲームの内側と外側の関係性を考えたいのか、なんらかのダイナミクスを考えるためのツールとしてゲームという概念を用いたいのか。あるいはそれらを複合的に位置づけるような見取り図を構築したいのか。

　カテゴリについての合意が難しいのと同様に、多層的なモデルを導入したとしても、どのような多層構造が適切かということについて決定的なモデルが提出できるというわけではない。

2.2.5.3  要素間の関係性の記述から、ネットワークへ

　つまり、「階層」は実在的な実態であるというよりは、何らかの説明において便宜的に導入される区別としての側面が強い。先に示したような階層を唯一の実態であるかのように論じようと思うと、根拠付けが難しい。自然科学であれば、物理レベル／化学レベル／生物レベルといった階層的説明がしばしばなされるが、本書で扱うのは人間の心的現象やその環境（ルールやゴール）である。そこに上下の階層性を想定することがどこまでできるかよくわからない。

　ただ様々な階層の区別において繰り返し提示されている要素群は類似している。たとえば、下記の要素はかなり多くの論者が繰り返し取り出している。

　（１）ルールなどの行為の環境（ルール、構造、メカニクス）
　（２）行為・実践それ自体、もしくは行為の環境と遊び手の都度の相互作用（行為、ダイナミクス）
（３）心的な現象（体験）あるいは意味解釈（表象）
（４）ゲーム文脈の内外を区別する枠（フレーム）

　もちろん、もっと細かく分けることもできる。ルールの周辺概念をどこまで含むのか。同じ心理的なプロセスを経るものであるにせよ、体験と表象を分けるべきか。ゲーム内外の区別をどのような概念によってつけるのか。相互作用の概念化にも多様な仕方がある（これらの詳細な議論は第三部以後で行う）。ただ、大枠のまとまりがいくつかあり、それらが相互に関係しているという程度のことは言えるだろう。果たしてそれらが上下の関係で素描することが可能なものなのかどうかは、わからない。

　ここで注目しておきたいのは、何よりも、様々な階層らしき要素の関係は、論者によって描き出し方が異なっており、仮にそれを図式化し、線と点の関係を引いていくとすれば、そこにはごちゃごちゃとしたネットワーク的な図式が現れる、ということだ。

　二層とも、三層とも、四層ともネットワークの構造について理解してもらうための簡単な図を例示しておこう[12]。

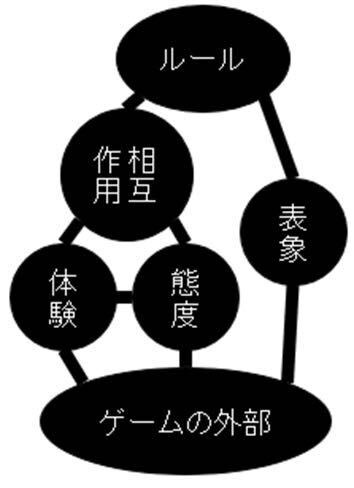
　このネットワーク図を上から下に目を移動させて右半分に着目すれば、三層にみえる。そして同じく上下関係の左半分に着目すれば四層にも見える。また、上下関係を見ずに左右に目を移動させてもらえれば、上をみると一層に。少し下を見ると二層に。さらに下を見れば三層にも見えるだろう。

　こういったネットワーク上に関係したものは、視点をどうとるかによって二層とも三層とも、四層とも捉えられうる状況がわかってもらえるだろうか。

　層の数が決定できないような現象を考えるときに、現象間のネットワークという考え方を採用すると、見通しがよくなるところがある。

　なお、この層と層の関係ネットワーク構造は、関係集合の重なりあいとして描きなおし相互に変換することもできる[13]。下記に、これを変換した図を示そう。 

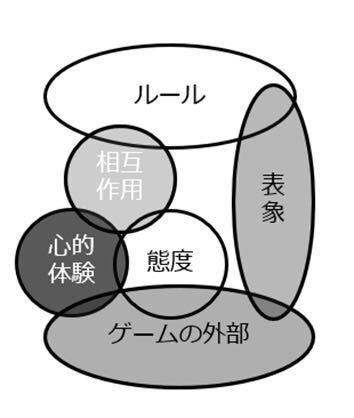
　こうした変換が可能であるということは、意味の共通した部分と、共通しない部分を論じるような概念範囲の集合論的な発想とも接続しうる[14]。意味や現象のネットワークを捉える、ということは話を複雑にしてしまっているようにも見えるかもしれない。ただ、話を単純化しようとして、議論が決定不可能になって、わけがわからなくなるぐらいであれば、ネットワークのような汎用性の高い形を考えるのは順当なアプローチだと言えるだろう。 

2.2.5.4  ネットワークの全体を考える

　遊びやゲームをめぐっては、概念間の関係を整理し、複雑なネットワークがどのように相互作用し維持されるかまで含めて論じようとした研究もある。サットン＝スミスやヘンリックスは、その代表例である。彼らは「遊び」を、複数の解釈システムが相補的に働き合うダイナミズムとして描こうとした[15]。あるときは学問分野ごとの文脈という解釈システムが概念の幅を規定し、あるときはその機能とプレイヤーの関係性が概念の展開の幅を規定する。

　こうした論者たちは「遊び」には、複数の典型があり、それらが相互に関係したり、なだらかに推移して別のものに変化するといった説明を試みている。これは、遊びやゲームの概念の典型が一つに集約されると考える手法（ユールの古典的ゲームモデルなど）とは異なる前提を持っている。

　この違いは「ゲームとは何か」についての、複数の回答をならべ、それを配置し、関係づけるときに、それらをどのようにして集約するかという方法論の違いだと言ってもいい。

　ある程度同一のものを指しているという前提で、特に共通して指摘される部分はどこになるかを確認していく手続きをとれば、「一つの典型」を確認するという形になるだろう。

　一方で、複数の典型があるという前提で、回答の差異に注目しながら全体像の記述を目指せば、「複数の典型」を示すという仕事になる。

　本書が検討したいのは、この双方を接続するようなことである。つまり、複数の典型というモデルをまず前提にすえつつ、それらの多様な典型がどのように関係しあいながら、全体のネットワークを構築し、総体として一纏まりに見えるような状態を成立させているのか、ということである。

　では、どのようにして、ネットワークの全体を考えていけばよいのだろうか。

2.2.5.5  ネットワークにおける中心～不均一が中心性をつくる～

　まず、ネットワークの構造について考えるための基本的な前提を確認したい。

次のような2つのネットワーク図を考えてみよう。それぞれA,B,C,D……とそれらを結ぶ線は先程の層と層の関係のようなものだと考えてほしい。A,B,C,D..は、たとえば、ルールのある活動、マジックサークルの成立、虚構、自由な活動……など適当なゲームの条件のようなものを思い浮かべてもらいたい。

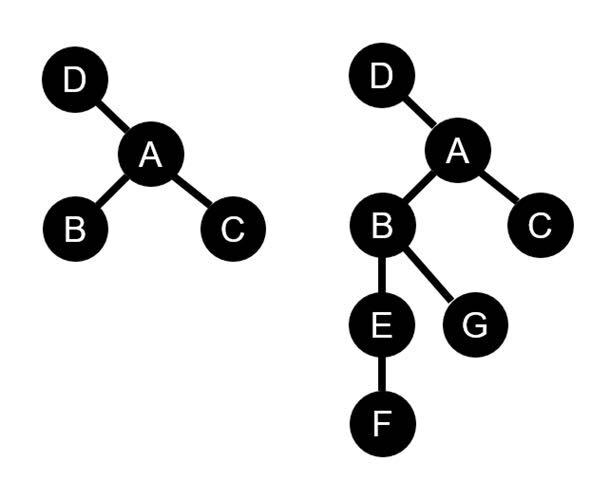
この左の図のネットワークの中心がどこにあるのかと言われれば、「A」が中心であることはほとんどの人が同意するだろう。異なる諸現象をつなぐ媒介となっている。

一方で、右の図の場合は少し難しい。

素朴に、つながっている線の数で判定すると、AとBが同じだけの線の数がある。この線の数はネットワーク論では、次数中心性と言われるものだ。

A：３（AB,AC,AD）
B：３（BA,BE,BG）
C：１（CA）
D：１（DA）
E：２（EB,EF）
F：１（FE）
G：1（GB）

　一方、媒介中心性は「別の点どうしをつなぐ通り道になっている度合い」を表す。直接つながっている線の数だけでなく、二次的に経由してつながっている線の数まで加えて考えると、BからつながっているEはさらにFを媒介している。このようなとき、Bは自身が直接つながっている数よりも、さらに広いものを媒介しているということができる。これが媒介中心的な点である。

　右の図は、左の図に比べると、ネットワークがごちゃごちゃとしていて、わかりにくい。このわかりにくいネットワークの中心がどこであるかは、「中心」の概念のとりかたによって変わる。そして、このごちゃごちゃとしたネットワークにおける中心性は、ネットワークの偏りにおいて見出される。このようなケースではネットワークが不均一になることで、中心性は失われるのではなく、媒介となる中心性をもった要素が新たに登場している[16]。

2.2.5.6  変化するネットワークの全体と中心

　ネットワークの構造が変化することで中心が変化することはゲーム『大航海時代』シリーズを遊んでみればよくわかる。はじまった直後は、ヨーロッパのどこかの港からスタートするが、基本的に手持ちの貿易船の性能が低いのでそこまで長距離の貿易ができない。このようなとき、比較的短い移動距離でたくさんの港と港を移動できるのが、地中海の都市だ。特にイタリアやギリシャあたりの都市は地中海の港と港の間を移動しようと思ったときに、中継地点としてとても利用しやすい。つまり、点（港）と線（航海）をつなぐネットワークの中心だ。イタリアやギリシャの都市は航海技術がそこまで発展していないときの中心地となる。

　次第に、大きな船を扱えるようになってくると、移動可能な距離が伸びて、今度は北米やアフリカまで移動できるようになる。つまり、北米やアフリカの多数の港（点）があらたにネットワークに接続されて、既存のネットワーク構造が歪むわけだ。こうなると、北米、アフリカ、ヨーロッパ各地への移動がしやすい港が新たなネットワークの中心となる。具体的には、リスボン（ポルトガル）やセビリア（スペイン）の使い勝手が非常によくなる。

　つまり、ここでは既存のネットワーク（地中海）の外部ネットワーク（北米やアフリカ）との関係によって中心が変化したということだ。外部との関係が中心を変化させるのだ。このネットワークの変化は実際の世界史で起こったことだ。ギリシャ、ローマの時代があり、大航海時代にはスペインやポルトガルが強力な力をもっていた。

　中心となるハブは、ネットワークの全てを説明するわけではないが、ネットワーク全体の特徴的な場所を説明するのには便利である。また、海運ネットワークの中心、陸運ネットワークの中心など、複数の中心が併存することも説明できる。

　このように、点（例えば観測点・拠点・話者・文脈など）から到達できる距離＝探索距離の広さによって、点どうしのつながりのネットワークが変化する。この発想を直観的に説明するモデルとして、トポロジーにおけるチェッホ複体（Čech complex）を参照しておこう。

　チェッホ複体では、各点の周囲に「探索可能な範囲」を表す円を仮定し、二つの円が重なっているとき、その二点の間に「関係が成立している」とみなして線を引く。こうして得られる点と線の集まりがネットワークを形作る。探索範囲の半径を連続的に変えることで、点どうしの結びつきが増減して、ネットワーク全体の形も変化していく。この「探索範囲を動かしながら、つながり方の変化を追う」という見取り図を概念化したものがチェッホ複体である[17]。

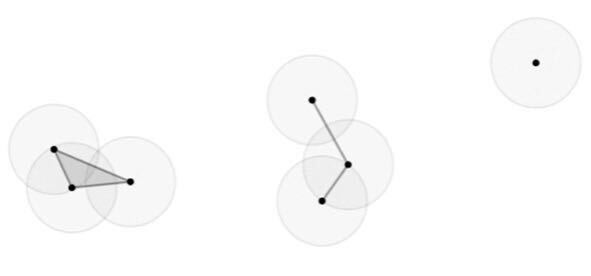
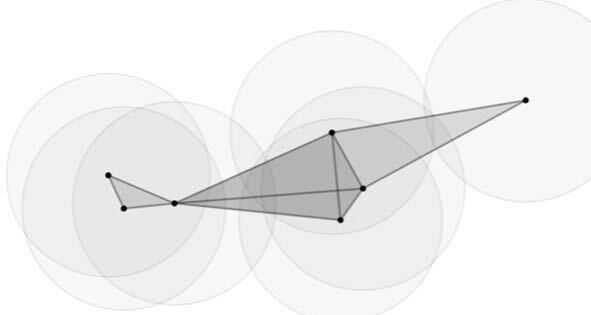
　チェッホ複体的なモデルは、概念の動的な変化についての可能な説明の一つだ。チェッホ複体のようなモデルを必ずしも仮定する必要はない。重要なポイントは、何らかのプロセスが媒介することで、ネットワークの構造の変化と、それに伴う中心の移動や多中心化といった事態が起こるということだ。

ネットワークの全体が安定的であれば、ネットワークの中心も安定しているが、ネットワークの全体が変化するならば、ネットワークの中心も変化しやすい。「ゲーム」の概念もその範囲が拡張されていくという性質を考慮すれば、その中心となるハブ的要素≒概念の中心も、これに伴って変化することがありうる。

　ゲームという現象の全体像は、ここ半世紀の間だけでも何度も変化している。デジタルゲームが普及し始めたときには、一人遊びの範囲が大きく増えた。小型のデジタルデバイスが普及するようになると、電車の移動時間など細切れな日常の時間の中にもゲームが広がりはじめた。こうした変化は「ゲーム」という現象の全体像を変化させるとともに、中心を変化させた可能性が高い。

　「ネットワークの中心性」は移ろいやすく、ネットワークの構造はしばしば中心となる位置を移動させる。逆に言えば、「中心」が安定的であるためには、ネットワークの範囲自体が安定的である必要があるが、ゲームの概念ネットワークが拡張変化をしやすい性質があるため、中心も、一定の不安定性にさらされていると言える。

　ゲームという概念がわかりやすい中心性をもたないのだとしたら、それはなぜなのか。このようなネットワーク的な整理は、単一の定義や固定的な階層構造では捉えきれない多様性と変化を説明する手がかりとなる。要素間の関係性とその動的な再編成として理解することで、より柔軟で説得力のある説明が可能になる。

　こうした、現象・意味のネットワークの変化のメカニズムを前提におきつつ、本書は学際的な議論の進め方を構築していくものだ。

[1] 実際には、低次／高次というよりは、ネットワーク上の概念かもしれないが、一定の条件下ではネットワーク上の概念であっても、低次／高次と記述してもほとんど問題ないことはあるだろうという前提にいったんここでは立つことにする
[2] Juul前掲書 p40
[3] クロス表の(1)と(2)の間の見えなくなっている部分にDがある
[4] この表は網羅的なものではなく例示的なものである。また、二層のモデルが三層のモデルよりも単純というわけでもない。たとえば、ステンロス(2015)は、「人工物／ゲームの活動」「活動としてのゲーム／遊び心」といった複数の区分を論じており、これは、構造・形式設計／活動／心的状態の三層モデルにできそうなところを、あえて三層にしないことも多い。
[5] Bogost, I. (2008). Unit operations: An approach to videogame criticism. MIT Press.
[6] Frans Mäyrä (2008). An introduction to game studies. SAGE, pp. 17–18.
[7] ノイマン、モルゲンシュテルン／銀林ら訳（2009）『ゲームの理論と経済行動』筑摩書房、pp. 138–139.
[8] 多木浩二（1995）『スポーツを考えるー身体／資本／ナショナリズム』ちくま新書.
[9] Walk, W., Görlich, D., & Barrett, M. (2017). Design, dynamics, experience (DDE): an advancement of the MDA framework for game design. In Game dynamics: Best practices in procedural and dynamic game content generation (pp. 27–45). Springer International Publishing.
[10] 松永訳(2016), pp. 45–52.
[11] Fine, G. A. (1983). Shared fantasy: Role playing games as social worlds. University of Chicago Press.
[12] これは、多層構造の決まりにくさを理解してもらうため図の例示であって、実態を示そうとしたものではない
[13] ただし、この変換は、集合の重なり合いが３つ以上になると、集合からネットワークへの変換は難しくなる。
[14] なお、こうした意味の集合と、意味のネットワークの相互の関係は意識されており、この関係はたとえば、下記に概説されている。Geeraerts, D. (2007, January). Family resemblances, radial networks, and multidimensional models of meaning. In Proceedings of the XXX AEDEAN Conference. Huelva: Publicaciones de la Universidad de Huelva.
[15] 清水(2004)と同様、サットン＝スミスもまたこうした発生機序についての説明を試みるものとしてはPiaget (1951)、Siegler(1996)、Linda Hughes（1983, 1988, 1989, 1991, 1993, 1993）などを評価している。
[16] グイド・カルダレリ、ミケーレ・カタンツァロ（高口太郎・増田直紀訳）「第五章 スーパーコネクター」、『ネットワーク科学―つながりが解き明かす世界のかたち―』(2014、丸善出版)
[17] 実際のネットワーク形成過程では、探索範囲が全点で一律に同じ大きさで変化するとは限らず、到達範囲も円形（球形）とは限らない。しかしここでは、探索距離という一つのパラメータを動かすと関係構造がどう変わりうるかを直観的に説明するためのモデルとして用いている。

この記事は、2026年1月19日に公開しました。本連載では、書籍に掲載される内容とは別に、連載としてはゲームに関わる多様なトピックを扱っていきます。概念間の関係性についての詳細な議論はぜひ書籍刊行をご期待ください！
これから更新する記事のお知らせをLINEで受け取りたい方はこちら。